From Euclidean to Mandelbrotian - Making System Art 'Natural'

4/15/2025, 5:59:59 AM | Jeanyoon Choi

Original Notes (Pre-LLM)

Scale - geoffrey west

자연세계에는 매끄러운 것이 없다 - 망델브로

모든 것이 울퉁불퉁…

매끈한 유클리드적 기하학을 넘어서, 매끈한 공산품적인 인터랙티브 아트를 넘어서

울퉁불퉁, 왔다갔다, Self-oscillating/self-existing/self-evolving system art?

Most modern 'systems' -- 네모의 꿈 -- 반듯한 유클리드식, Deterministic, Finite Scenarios

Also interactive art -- Just accommodates the interaction simply, no more dimension… Far from the real, more of fake -- 공산품과 같이.

What I want: From Euclidean to Mandelbrotian, From linear to non-linear, From flatness to non-flatness, From 1-Dimension to 2-Dimension, From 2-Dimension

Seven States of Randomness - Mimicking the real-world system! The trading system! The volatility! Every metric vibrates and moves every second -- it never stays stable! Even though there is no user interaction -- does not mean that system output stays stable. It always VIBRATES! It always moves! Like a fucking brownian motion, or even more wild -- IT ALWAYS OSCILLATES, MOVES, ALTERS, it never stays table. That is what makes the system art alive. That is what makes interactive art alive. The fact that there is no interaction does not mean the output should stay stable -- Output should be still be moving!

Interaction starts: t1, Interaction ends: t2

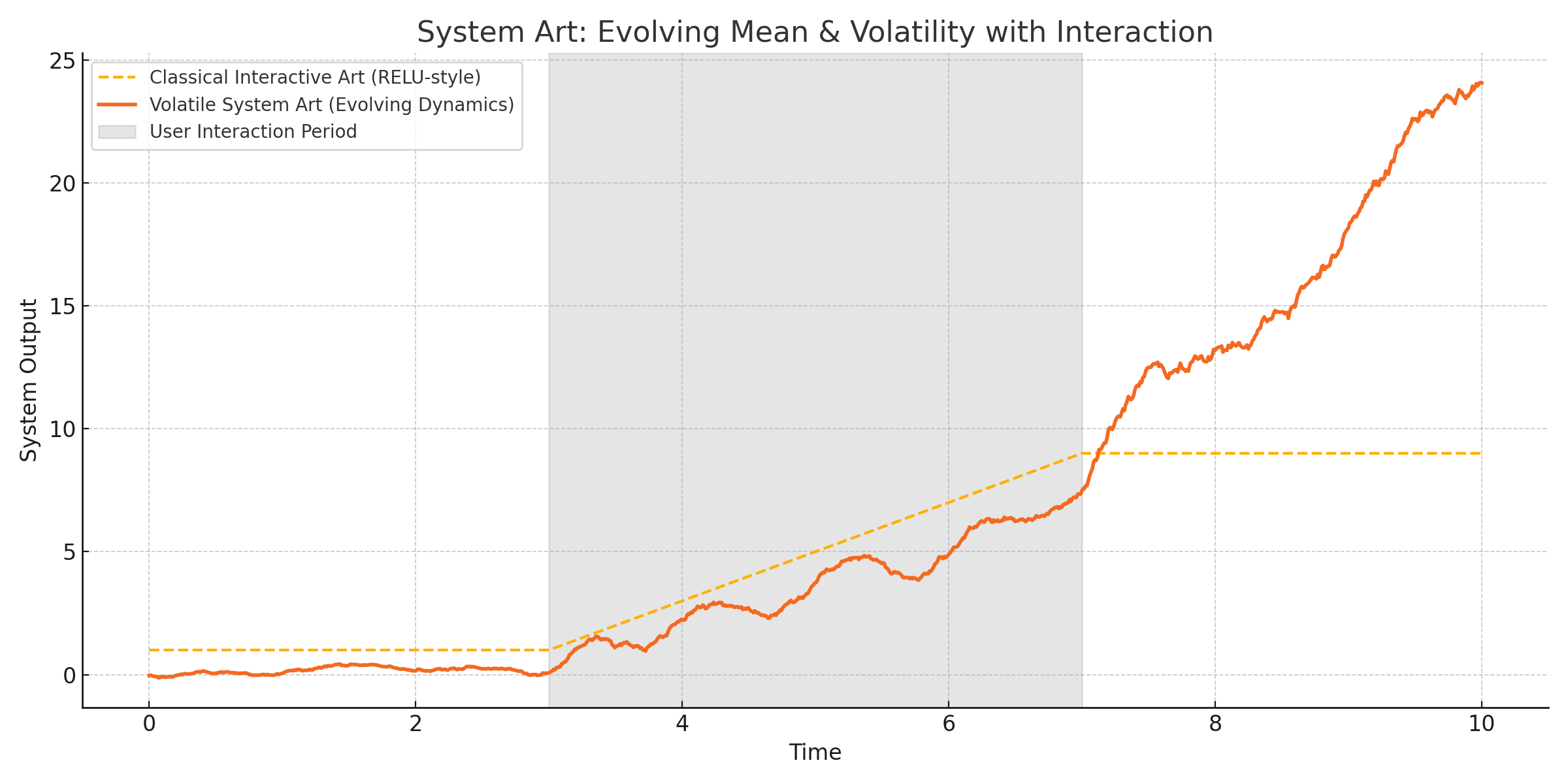
Previous system/interactive art: Operates as RELU.

f(t) = C1 (t < t1), C1 + t * k, C2 (t > t2)

What i offer: "Natural", Stochastic System

f(t) = q(t) (Quantum/Stochastic movement), q(t) + t * k(t) (Kinetic function -- adjusted accordingly to the user interaction), q'(t) (New stochastic movement after user interaction)

Good reference: Stock Graph. Stock graph after significant event (gov' policy, for example - an interaction). Or the weather. Smth ecological, hyperobject!

Volatility! Volatility! Volatility!

매끈한 선은 더이상 자연세계를 대변하지 못한다!

This is also the difference between object vs. system and simple system vs. automatic system.

Object: Stays the same. Even though it's interactive, it only handles the 'finite scenario'. Same interaction occurs: Ends up at same output.

System: Dynamic. Not only in terms of accommodating simple interactions, but an interaction stochastically/dynamically change the system - not only its external/surface-level 'state's, but also inner 'mechanisms' (how the system is inter-related/inter-twined)

Simple System: Stays static when not powered. It might be systematical, but it stays solid without any interaction.

Automatic System: It's 'automatic': IT EVOLVES AND CHANGES CONTINUOUSLY & AUTOMATICALLY even without any external interaction/input. It's ever evolving, ever changing, ever ever ever….

Touch Designer - Noise

Why do people incorporate noise node in touch designer? TO mimic nature, to mimic the uncertainty/randomness of nature, to make it look more 'natural'... But this is definitely not enough! Also the noise that I'm interested -- is not merely a 'visual' noise. More of 'system' noise, noise within the system, noise within the semantic interaction.

Now the big question: How to mimic such 'natural' circumstance within system art?

- Strategy 1. Mimicking Randomness: Just like TouchDesigner Noise… Easy Fix. But there is a clear limitation.

- Strategy 2. Real simulation happening: Let's say, multiple agents, 'beings', algorithms acting/trading/relating in real-time. Very stochastically - like Brownian motion? How to stimulate the behaviour of multi-agents? Computational power?

- Strategy 3. Using mathematical modelling of 2: Brownian motion, for example. Normal Distribution sometimes? If you cannot simulate N(=1000) agents in real-time (cuz of computational power limitation), at least use a mathematical model telling you the commonly observed behaviour of such grouping -- rather than merely just using random.

Any reference to system dynamics/system modelling?

"By unifying these references—mathematical, computational, aesthetic—you can engineer the kind of "natural, stochastic system" you describe: a system that does not "wait" passively for interaction but continues to mutate, swirl, and morph, as if it were alive."

English Version (LLM-Generated)

Title: From Deterministic Lines to Dynamic Complexity in System Art

In the natural world, nothing is perfectly smooth—a concept famously noted by Mandelbrot. Nature is characterized by rough, irregular patterns that defy the neat, Euclidean geometries often seen in conventional digital and interactive art. Modern systems of art and design tend to follow deterministic, finite, and linear scenarios; even interactive art is frequently confined to predetermined responses, creating outputs that, while responsive, ultimately lack the inherent dynamism of natural phenomena.

I propose a shift from the Euclidean to the Mandelbrotian, from linear to non-linear, from flatness to multi-dimensionality. Rather than relying solely on limited finite interactions, art should embrace the vibrancy and inherent unpredictability of real-world systems. Consider the behavior of financial markets for inspiration—after a significant event, such as a government policy change, a stock graph pulsates with volatility, its every metric fluctuating by the second. Even without explicit user input, these systems are never static; they are reminiscent of Brownian motion, in which continuous, random fluctuations convey a sense of life and organic motion.

Traditional interactive art often employs predetermined scenarios. For example, if an interaction begins at time t₁ and ends at time t₂, the system might operate along a simple, piecewise linear function:

  f(t) = C₁ when t < t₁, then C₁ + t · k during the interaction, followed by C₂ when t > t₂.

In contrast, my approach advocates for a "natural," stochastic system characterized by equations such as:

  f(t) = q(t) for the natural, quantum-like stochastic movement,

  q(t) + t · k(t) to adjust kinetically based on user interaction, and

  q′(t) to represent the renewed stochastic dynamics after interaction.

This model echoes the behavior of stock market graphs following significant events or changes in weather conditions—systems defined by their inherent volatility.

This idea also underscores the distinction between objects and systems in art. An object remains static; even if its interaction is designed to respond in some way, the end result is predictable, following a finite scenario. A system, on the other hand, is dynamic by nature. Its interactions induce changes not only on a surface level but also within its inherent mechanisms—altering internal relationships and evolving over time. Moreover, a simple system may remain static when unpowered, while an automatic system continues to evolve and morph continuously, even in the absence of external input.

For instance, consider the use of noise nodes in TouchDesigner. Artists often incorporate these nodes to simulate the inherent uncertainty and randomness of natural processes, achieving a more "organic" aesthetic. However, the noise I envision extends beyond mere visual randomness; it is the internal, systemic noise—an integral part of the semantic interaction within the system.

Achieving a natural, stochastic system in art poses several challenges:

  • Strategy 1 involves mimicking randomness using tools like TouchDesigner’s noise functions. This approach is straightforward but inherently limited.

  • Strategy 2 aims for real-time simulation using multiple agents or algorithms that interact in a stochastic manner similar to Brownian motion. While this method can yield rich, emergent behavior, it is computationally intensive.

  • Strategy 3 utilizes mathematical modeling of multi-agent systems (such as those following a normal distribution) to approximate observed behaviors. This approach offers a practical alternative when real-time simulation is limited by computational constraints.

By integrating mathematical precision, computational algorithms, and aesthetic considerations, it is possible to engineer a truly natural, stochastic system. This system does not passively await interaction; rather, it continuously mutates, swirls, and morphs as if it were alive—a system that embodies the inherent volatility of the real world.

Volatility is not a defect—it is an essential characteristic of natural systems. Smooth, predictable lines no longer suffice to represent the intricacy and dynamism of the natural world. Instead, embracing complexity and randomness offers a pathway to creating art that is as alive and ever-changing as nature itself.

Korean Version (LLM-Generated)

다음은 원문 내용을 보다 전문적이고 체계적으로 재구성한 한국어 버전입니다.

─────────────────────────────

제목: Scale – Geoffrey West

─────────────────────────────

자연계에는 완전히 매끄러운 현상은 존재하지 않는다 – 망델브로의 말처럼, 우리 주위의 모든 것은 본질적으로 울퉁불퉁하다.

우리는 전통적인 유클리드 기하학의 단순하고 매끄러운 형태를 넘어서, 공산품처럼 일정한 인터랙티브 아트를 넘어 새로운 차원의 시스템 예술을 모색하고자 한다. 이러한 예술은 단순한 상호작용을 넘어 스스로 진동하고, 존재하며, 진화하는 (Self-oscillating / Self-existing / Self-evolving) 특성을 가져야 한다.

현재 다수의 현대 시스템과 인터랙티브 아트는 일정한(Deterministic) 유클리드적 틀, 즉 정사각형 같은 고정된 시나리오 내에서 동작한다. 이들 작품은 상호작용을 단순히 수용하는 정도에 머물며, 결과적으로 현실 세계와는 거리가 먼 인공적인 결과를 낳는다.

내가 추구하는 방향은 다음과 같다.

유클리드적(finite, linear) 관점에서 망델브로적인 복잡성으로, 1차원에서부터 평면을 넘어 다차원적(non-flat) 성질을 포함하는 비선형 시스템으로의 전환.

─────────────────────────────

일곱 단계의 무작위성 – 현실 세계 시스템의 모방

─────────────────────────────

현실의 거래 시스템과 같이 매 순간 변동하는 불안정한 상황을 재현하고자 한다. 실제 거래 시스템은 사용자 상호작용 여부와 무관하게 끊임없이 진동하며 움직인다. 이는 단순히 사용자 상호작용이 없어서 안정된 결과를 내야 한다는 기존 관념을 깨뜨린다. 한 예로, 상호작용이 시작되는 시점(t1)과 종료되는 시점(t2) 사이에서 기존의 인터랙티브 아트는 다음과 같이 작동할 수 있다.

기존 방식:

  f(t) = C1    (t < t1)

  f(t) = C1 + k · t   (t1 ≤ t ≤ t2)

  f(t) = C2    (t > t2)

내가 제안하는 “자연적” 확률 시스템은 다음과 같이 동작한다.

  f(t) = q(t)       (양자적/확률적 움직임)

  f(t) = q(t) + k(t) · t   (사용자 상호작용에 따른 변화율 조정)

  f(t) = q′(t)      (상호작용 후 새로운 확률적 움직임)

주식 시장의 그래프나 주요 사건(예: 정부 정책 변화) 후의 주가 움직임, 또는 날씨와 같이 끊임없이 변동하는 생태학적 현상을 참고할 수 있다. 요컨대, 시스템 자체는 변동성과 불확실성을 내포해야 하며, 매끄러운 곡선은 더 이상 자연 세계의 본질을 대변할 수 없다.

─────────────────────────────

객체와 시스템, 그리고 단순 시스템과 자동 시스템의 차이

─────────────────────────────

• 객체(Object): 객체는 고정된 성질을 유지한다. 비록 상호작용이 가능하더라도 한정된 시나리오 내에서 작동하며, 동일한 입력은 동일한 출력을 만들어낸다.

• 시스템(System): 시스템은 동적이다. 단순한 상호작용 수용에 그치지 않고, 상호작용이 발생하면 시스템의 외부 상태 뿐만 아니라 내재적 메커니즘까지 확률적으로 또는 동적으로 변화시킨다.

또한,

• 단순 시스템(Simple System): 전원이 꺼지면 고정된 상태를 유지하는 시스템이다.

• 자동 시스템(Automatic System): 외부 입력 없이도 지속적으로 스스로 진화하고 변화하는 시스템으로, 끊임없이 진행되는 변동성을 지닌다.

─────────────────────────────

Touch Designer의 노이즈 – 자연 모방의 한계와 그 너머

─────────────────────────────

Touch Designer에서 노이즈 노드를 사용하는 이유는 자연의 불확실성과 무작위성을 시각적 요소로서 모방하기 위함이다. 그러나 내가 추구하는 노이즈는 단순한 시각적 왜곡을 넘어, 시스템 내부의 불가피한 ‘소음’과 상호작용의 본질적 무작위성을 구현하는 것이다.

─────────────────────────────

문제 제기 및 전략

─────────────────────────────

문제: 어떻게 하면 시스템 아트 내에서 ‘자연적인’ 상황과 동적 불확실성을 효과적으로 모방할 수 있을까?

전략:

① 무작위성 모방 – Touch Designer의 노이즈와 같이 상대적으로 간단한 해결책이 존재하지만, 그 한계는 명백하다.

② 실시간 다중 에이전트 시뮬레이션 – 다수의 알고리즘적 존재들이 실시간으로 상호작용하며 거래 혹은 관계를 형성하는 방식으로 복잡한 동적 시스템을 구동. 그러나 이는 높은 계산 성능이 필요하다.

③ 수학적 모델링 활용 – 예를 들어 브라운 운동이나 정규 분포와 같은 수학적 모델을 통해 다수의 에이전트 집단이 보이는 일반적인 행동 양식을 재현할 수 있다. 만약 수많은 에이전트를 실시간으로 시뮬레이션하는 것이 계산 성능의 한계로 불가능하다면, 이러한 수학적 모델은 더욱 효과적 대안이 될 수 있다.

─────────────────────────────

참고 및 결론

─────────────────────────────

수학적, 계산적, 그리고 미학적 접근법을 통합함으로써 ‘자연적이며 확률적인 시스템’을 설계할 수 있다. 이러한 시스템은 단순히 외부 상호작용을 수동적으로 기다리는 것이 아니라, 마치 살아있는 듯 스스로 변화하고 회오리치며 끊임없이 진화한다.

이와 같이, 전통적인 고정적 인터랙션 모델을 넘어 지속적으로 진동하고 변화하는 자연계의 다층적 특성을 반영하는 시스템 및 인터랙티브 아트를 구현하는 것이 현대 예술의 새로운 방향성이 될 수 있다.

Tags

Text written by Jeanyoon Choi

Ⓒ Jeanyoon Choi, 2024